Question

如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D．下列结论：①AC∥OD；②△OBD是等边三角形；③S_△OBD=BC•OE；④若BC=8，DE=2，则AB=10．其中正确的结论有（ ）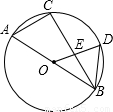

A．①②
B．①②④
C．①④
D．②③④

Answer 1

【答案】分析：根据圆周角定理、垂径定理和勾股定理分析求解后直接选取答案．
解答：解：∵AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D，
∴∠ACB=90°，CE=BE，
∠OEB=∠DEB=90°，
①AC∥OD，正确；
②OD=OB，△ODB是等腰三角形，错误；
③S_△OBD=S_△OBE+S_△DBE=BE•OE+BE•DE=BE（OE+DE）=×BC•OD=BC•OD，错误；
④若BC=8，DE=2，设OD=r，则OE=r-2，AB=2r，AC=2OE=2（r-2），在Rt△ABC中，AC²+BC²=AB²，
即[2（r-2）]²+8²=（2r）²，解得r=5，∴AB=2r=2×5=10，正确．
因此①④正确．
故选C．
点评：此题较复杂，解答此题关键是要熟知以下概念：垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．圆周角定理：直径所对的圆周角是直角．