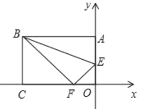
题目内容
【题目】长方形纸片![]() 中,
中,![]() ,
,![]() ,把这张长方形纸片
,把这张长方形纸片![]() 如图放置在平面直角坐标系中,在边
如图放置在平面直角坐标系中,在边![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处.
处.
(1)点![]() 的坐标是____________________;点
的坐标是____________________;点![]() 的坐标是__________________________;
的坐标是__________________________;
(2)在![]() 上找一点
上找一点![]() ,使
,使![]() 最小,求点
最小,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一个动点,设
上一个动点,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数 关系式.
的函数 关系式.
【答案】(1)(0,3);(﹣4,0);(2)![]() ;(3)
;(3) ![]()
【解析】
(1)根据折叠性质求出BF,再利用勾股定理求出CF,从而得出OF,在△EOF中设未知数的方法根据勾股定理列出方程求解即可.
(2)作E关于AB的对称点,连接对称点到F,利用勾股定理求出长度即可.
(3)利用待定系数法求出PF的表达式,再根据面积公式代入即可.
(1)由折叠的性质可得BF=AB=10,
∵BC=8,∠BCF=90°,
∴CF=![]() ,
,
∵OC=AB=10,
∴OF=10-6=4,即F的坐标为(﹣4,0),
设AE为x,则EF也为x,EO为8-x,
根据勾股定理得:42+(8-x)2=x2,解得x=5.
∴EO=8-5=3,即E的坐标为(0,3).
(2)作E关于AB的对称点E’,连接E’F交AB于P,此时E’F即为PE+PF最小值.

根据对称性可知AE’=AE=5,则OE’=5+8=13,
根据勾股定理可得:E’F=![]() .
.
(3)根据题意可得S=![]() .
.
设直线PF的表达式为:y=kx+13,
将点F(﹣4,0)代入,解得k=![]() ,
,
∴PF的表达式为:![]() ,
,
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目